
こんにちは。
テービーテックの村松です。
最近は「本日の関数」というちまちましたものを連日投稿していましたが、
本日は多少厚みのある内容になっている、はずです。
題名の通り、Kaggleに挑戦し始めました。
とは言え、お決まりの「Titanic: Machine Learning from Disaster」。
タイタニック号の乗客の生存予測に取り組む練習課題です。
Kaggleについての詳しいことは深津パイセンも紹介してますので、ご参照くださいませ。
ds-blog.tbtech.co.jp
さっそくやってみよう
データの読み込み
こちらから
・train.csv
・test.csv
をダウンロードしてきます。
同じ場所に提出ファイルの例(gender_submission.csv)もありますので提出前に確認しましょう。
#必要なライブラリのインポート import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns sns.set() #データの読み込み train_data = pd.read_csv('train.csvのパス')#学習用データ test_data = pd.read_csv('test.csvのパス')#テストデータ
中身の確認
では早速中身を確認していきましょう。
train_data.head(3)
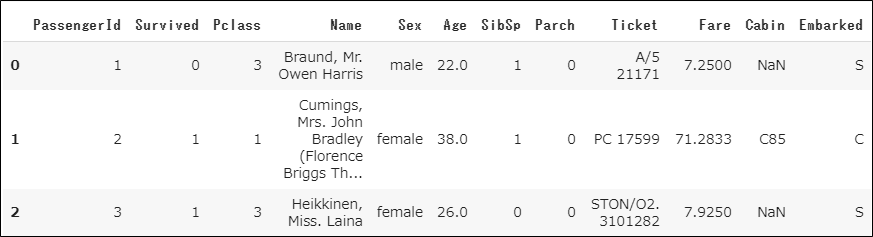
test_data.head(3)

test_dataはターゲットとなるSurvivedがないので1列少ないですね。
列名は左から
・PassengerId:乗客のID
・Survived:生存フラグ(0:死亡・1:生存)←今回はこれを予測します
・Pclass:チケットクラス(1~3)
・Name:名前
・Sex:性別
・Age:年齢
・SibSp:タイタニック号に乗っている兄弟/配偶者の数
・Parch:タイタニック号に乗っている親/子供の数
・Ticket:チケット番号
・Fare:料金
・Cabin:客室番号
・Embarked:乗船港(C:Cherbourg・Q:Queenstown・S : Southampton)
Kaggleではデータの説明が書いてあるのですが、SibSpのメモに
「愛人と婚約者は無視されました」
とあったのがなんともリアリティを感じました。
男女で同じ客室番号なのに配偶者がいなかった時は愛人か婚約者って思っておけばいいんですかね。
では、中身を細かく見ていきましょう。
各項目と生存率の関係
各項目とSurvivedをグラフ化したりして比較していきます。
- PassengerId
乗客それぞれの固有のIDです。
生存率との関係性は、他の要素との関連性を見つけられれば使い道がある、かもしれません。
今回は保留とします。
- Pclass
sns.countplot(train_data['Pclass'], hue=train_data['Survived'])
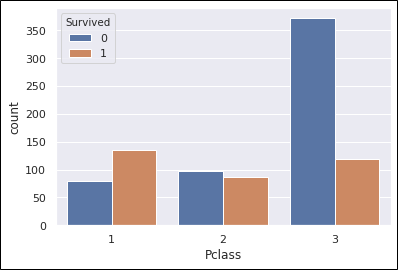
それぞれの生存率を計算してみます。
s_pclass = train_data['Survived'].groupby(train_data['Pclass']).mean() s_pclass
#output Pclass 1 0.629630 2 0.472826 3 0.242363 Name: Survived, dtype: float64
チケットクラスは
1:お金持ち
2:普通
3:労働階級
という感じの分類になります。
わかりやすいくらい3の乗客の死亡率は高いですね。
- Name
train_data['Name'].head(20)
#output 0 Braund, Mr. Owen Harris 1 Cumings, Mrs. John Bradley (Florence Briggs Th... 2 Heikkinen, Miss. Laina 3 Futrelle, Mrs. Jacques Heath (Lily May Peel) 4 Allen, Mr. William Henry 5 Moran, Mr. James 6 McCarthy, Mr. Timothy J 7 Palsson, Master. Gosta Leonard 8 Johnson, Mrs. Oscar W (Elisabeth Vilhelmina Berg) 9 Nasser, Mrs. Nicholas (Adele Achem) 10 Sandstrom, Miss. Marguerite Rut 11 Bonnell, Miss. Elizabeth 12 Saundercock, Mr. William Henry 13 Andersson, Mr. Anders Johan 14 Vestrom, Miss. Hulda Amanda Adolfina 15 Hewlett, Mrs. (Mary D Kingcome) 16 Rice, Master. Eugene 17 Williams, Mr. Charles Eugene 18 Vander Planke, Mrs. Julius (Emelia Maria Vande... 19 Masselmani, Mrs. Fatima Name: Name, dtype: object
Nameは今回は保留。
ただ、カンマ区切りの真ん中の単語に規則性がありそうなことがわかります。
性別と年齢とかに関係してそうですね。
うまく抜き出せれば説明変数に使えそうです。
- Sex
sns.countplot(train_data['Sex'], hue=train_data['Survived'])
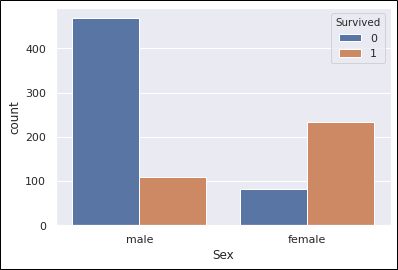
生存率を計算。
s_sex = train_data['Survived'].groupby(train_data['Sex']).mean() s_sex
#output Sex female 0.742038 male 0.188908 Name: Survived, dtype: float64
こちらも非常にわかりやすいですね。
女性の避難が優先されたことがわかります。
- Age
#年代「n_interval」のカラムを追加 train_data['n_interval'] = pd.cut(train_data['Age'], bins=np.arange(0, 100, 5), right=False) #年代ごとの生死を比べます plt.figure(figsize=(15, 5)) sns.countplot(train_data['n_interval'], hue=train_data['Survived']);
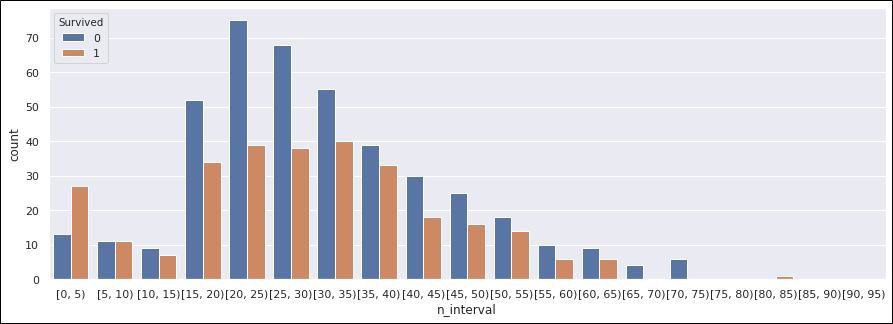
生存率の計算。
s_interval = train_data['Survived'].groupby(train_data['n_interval']).mean()
#output n_interval [0, 5) 0.675000 [5, 10) 0.500000 [10, 15) 0.437500 [15, 20) 0.395349 [20, 25) 0.342105 [25, 30) 0.358491 [30, 35) 0.421053 [35, 40) 0.458333 [40, 45) 0.375000 [45, 50) 0.390244 [50, 55) 0.437500 [55, 60) 0.375000 [60, 65) 0.400000 [65, 70) 0.000000 [70, 75) 0.000000 [75, 80) NaN [80, 85) 1.000000 [85, 90) NaN [90, 95) NaN Name: Survived, dtype: float64
性別と併せて女子供の避難が優先されたことが伺えますね。
- SibSp
sns.countplot(train_data['SibSp'], hue=train_data['Survived'])
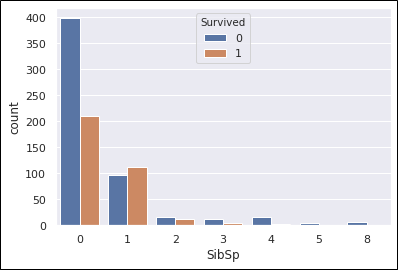
生存率の計算。
s_sib = train_data['Survived'].groupby(train_data['SibSp']).mean()
#output SibSp 0 0.345395 1 0.535885 2 0.464286 3 0.250000 4 0.166667 5 0.000000 8 0.000000 Name: Survived, dtype: float64
伴侶が複数いるのは稀な気がするので2以上はきょうだいと考えるのが普通ですよね。
家族が一緒に行動していて大人数なほど死亡率が高い、ということでしょうか。
- Parch
sns.countplot(train_data['Parch'], hue=train_data['Survived'])
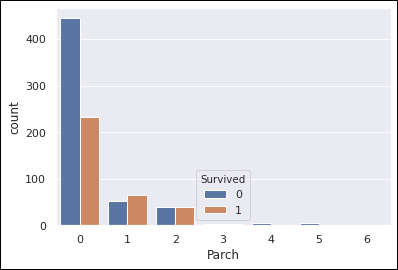
生存率の計算。
s_par = train_data['Survived'].groupby(train_data['Parch']).mean() s_par
#output 0 0.343658 1 0.550847 2 0.500000 3 0.600000 4 0.000000 5 0.200000 6 0.000000 Name: Survived, dtype: float64
親というより子供と同伴ってことで生存率が上がっているような気がしますね。
あまり大人数だと逆効果の可能性もありますね。
- Ticket
こちらも名前と同じく規則性を見つけることができれば使えそうですが、今回は保留とします。
- Fare
単純に考えるとチケットクラスと関係が深そうですかね?
先にそちらを確認してみましょう。
#そのままヒストグラムを作ると右にとても長い偏ったグラフになったので対数変換してからグラフ化します。 plt.figure(figsize=(15, 8)) sns.distplot(np.log1p(train_data[train_data['Pclass']==1]['Fare']),kde=False,rug=False,bins=10,label='1') sns.distplot(np.log1p(train_data[train_data['Pclass']==2]['Fare']),kde=False,rug=False,bins=10,label='2') sns.distplot(np.log1p(train_data[train_data['Pclass']==3]['Fare']),kde=False,rug=False,bins=10,label='3') plt.legend()
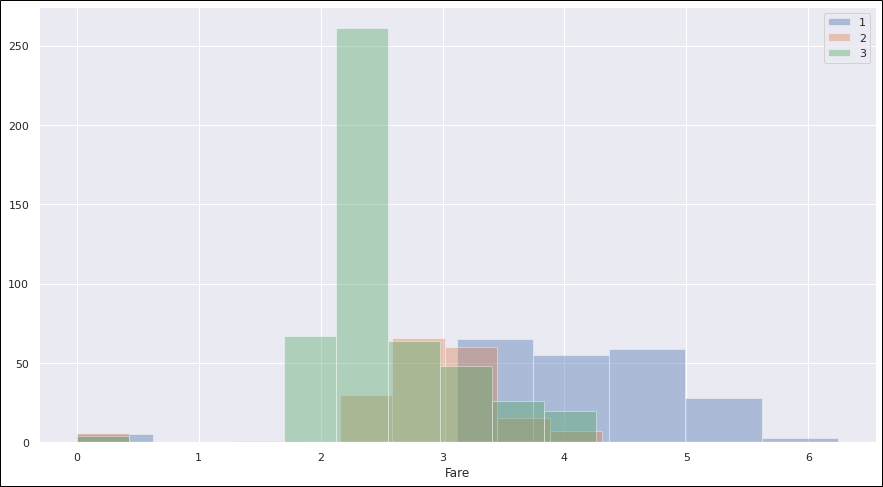
概ねチケットランクに準じている印象です。
では、次は料金と生死を比べてみましょう。
plt.figure(figsize=(15, 8)) sns.distplot(np.log1p(train_data['Fare']),kde=False,rug=False,bins=10,label='Fare') sns.distplot(np.log1p(train_data[train_data['Survived']==1]['Fare']),kde=False,rug=False,bins=10,label='Survived') sns.distplot(np.log1p(train_data[train_data['Survived']==0]['Fare']),kde=False,rug=False,bins=10,label='Death') plt.legend()
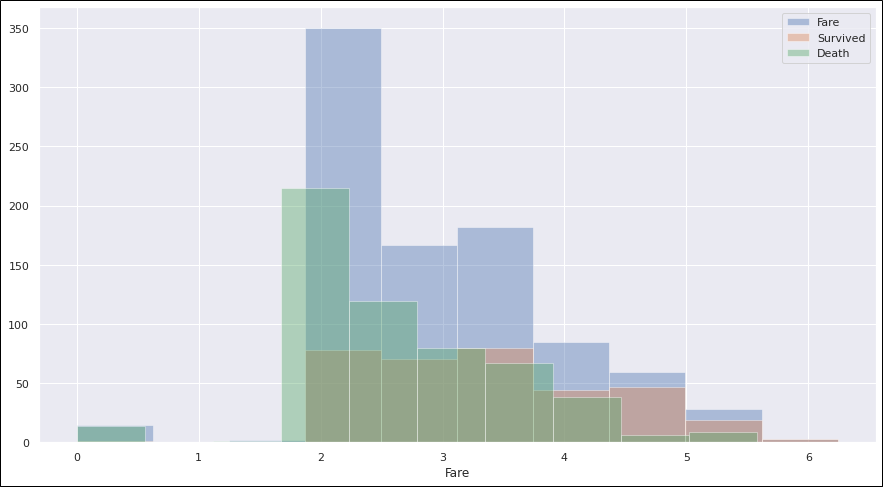
DeathとFareのグラフは似た形になっていますね。 死亡率と関係がありそうです。 とてもたくさんお金を払っている人の生存率は高そうですが、それだけが生死に関係しているわけではなさそうですね。
- Cabin
欠損値を確認したところ今回は欠損が多いため保留とします。
ただ、頭文字が客室の階層を表しているため救命ボートとの距離に近いほど生存率が高いという人もいました。
参照:Titanic: Machine Learning from Disaster | Kaggle
逆に情報が不確かであることを理由に説明変数から外す人もいました。
参照:Cabin Allocations
- Embarked
sns.countplot(train_data['Embarked'], hue=train_data['Survived'])
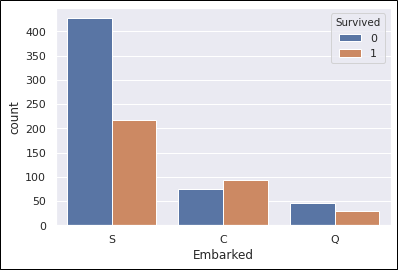
生存率の計算。
s_em = train_data['Survived'].groupby(train_data['Embarked']).mean() s_em
#output Embarked C 0.553571 Q 0.389610 S 0.336957 Name: Survived, dtype: float64
まさか乗船港で差が出ると予想していなかったので一瞬驚いたのですが、
乗船港ごとのチケットランクを確認して納得しました。
sns.countplot(train_data['Embarked'], hue=train_data['Pclass'])
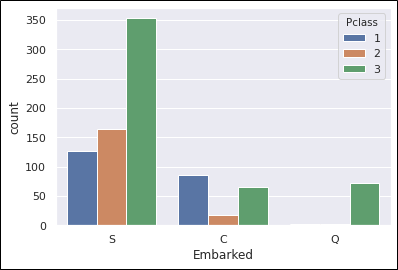
そりゃ港によって集まる人に特色出るわな。
なるほど、Cはお金持ちの比率が高いので生存率も高かったのでしょう。
ざざっとそれぞれの項目が生死に関わりがあるかどうかを確認してきました。
・年齢
・性別
・支払っている料金(もしくは社会的階級)
このあたりがわかりやすく生存率に関係していそうですね。
他の項目は上記の3つに関連があるかないか、といった印象です。
さて、逐一コードとグラフを載せたら長く長りましたので一度ここで区切ります。
次回は前処理からKaglleにコミットするまでをご紹介します。
また、今回のコード内で使用している関数についても「本日の関数」シリーズでぼちぼち紹介していきますのでお楽しみに。